Beweis für den Satz zum Umkreisradius eines Dreiecks

Gegeben sei ein Dreieck ABC mit dem Umkreis und dem Umkreismittelpunkt U.
Es soll gezeigt werden, dass 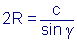        gilt.

1. Zunächst wird der Durchmesser AP des Umkreises ausgehend von A eingezeichnet. Betrachte nun das Dreieck APB. Die Seite AP hat als Durchmesser des Umkreises die Länge 2R.
   

2. Die Seite AB ist eine weitere Seite des Dreiecks APB und hat die Länge c.
   
   
3. Der Eckpunkt B liegt auf einem Halbkreis über dem Durchmesser AP (Thaleskreis). Der Winkel ABP muss daher ein rechter Winkel sein.
   
   
4. Die Punkte C und P liegen auf einem gemeinsamen Kreisbogen über der Sehne AB. Wegen des Peripheriewinkelsatzes müssen der Winkel ACB und der Winkel APB gleich groß sein. Überzeuge dich davon, indem du den Eckpunkt C entlang des Kreisbogens verschiebst. Beobachte dabei die beiden Winkel. Für den Winkel APB gilt daher:   φ = γ.
   
   
5. Daher gilt im (rechtwinkligen) Dreieck APB:                                         
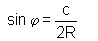
   Wegen  φ = γ gilt auch im (beliebigen) Dreieck ABC: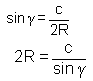                         
   Aus dem Sinussatz folgt daraus für jedes beliebige Dreieck: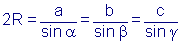                

© 2014 Verlag E. DORNER, Wien; Dimensionen - Mathematik 5; erstellt mit GeoGebra