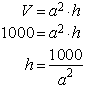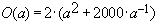Minimale Oberfläche einer Getränkeverpackung

Eine Verpackung für Saft hat die Form eines Quaders mit quadratischer Grundfläche.

Aufgabe
Bewege den roten Punkt B entweder in der 3D-Ansicht oder in der zweidimensionalen Ansicht des Netzes. Dadurch veränderst du die Länge der Seitenkante a des Basisquadrats der Verpackung.
Blende mit dem Kontrollkästchen die Zielfunktion für den Flächeninhalt der Oberfläche ein.
Lies aus dem Graphen ab, bei welcher Länge a der Oberflächeninhalt für eine 1-Liter-Packung (V = 1000 cm³) minimal wird.
Berechne anschließend das Minimum des Oberflächeninhalts mit dem CAS oder verfolge die einzelnen Rechenschritte im Anschluss an das Applet.

Hinweis: Beachte, dass in dem Applet Rundungsfehler auftreten können.

Oberfläche = Grundfläche + Mantel + Deckfläche	O = G + M + D = 2·G + M	▼
Wahl der Bezeichnung für die Variablen a und h:		▼
Nebenbedingung beachten: Die Höhe h kann aus dem gegebenen Volumen V berechnet werden		▼
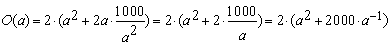
Aufstellen der Zielfunktion:	Zielfunktion Die Bezeichnung O(a) bringt zum Ausdruck, dass die Zielfunktion nur mehr von einer Variablen, nämlich der Seitenkante a, abhängt.	▼
Vereinfachte Zielfunktion Das Weglassen eines gemeinsamen Faktors vereinfacht die Zielfunktion.	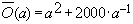Die Eigenschaft, an welcher Stelle a der Oberflächeninhalt minimal ist, wird dadurch nicht  beeinflusst.	▼
Ableiten der (vereinfachten) Zielfunktion:		▼
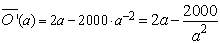1. Ableitung gleich null setzen:		▼
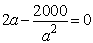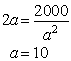
Gleichung lösen:	h = V/a² = 1000/10² = 10 cm;   O(10) = 600 cm² Es handelt sich um einen Würfel mit Seitenkante 10 cm.	▼
2. Ableitung für Unterscheidung Maximum bzw. Minimum: Beachte: Bei der Berechnung mit dem CAS wurde im Applet nicht mit der vereinfachten Zielfunktion gerechnet. O''(10) ist deshalb 12.	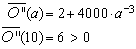=>  Minimum	▼
Antwort formulieren:	Der minimale Oberflächeninhalt von 600 cm² entsteht bei einer Seitenkante mit a = 10 cm.

  © 2016 Verlag E. DORNER, Wien; Dimensionen - Mathematik 7; erstellt mit GeoGebra