Minimale Oberfläche einer Dose mit gegebenem Volumen
Eine Dose für Gemüsemais hat die Form eines Zylinders.
Aufgabe
Verändere mit dem Schieberegler den Radius r der Dose.
Lies aus dem Graphen
ab, bei welchem Radius r für ein Volumen von V = 425 cm³ der
Oberflächeninhalt minimal wird.
Verändere das Volumen auf
V = 1000 cm³. Für welchen Radius r wird in diesem Fall der
Oberflächeninhalt minimal?
Berechne anschließend das Minimum des Oberflächeninhalts für ein
beliebiges Volumen V und das Verhältnis von r und h.
Dose (reale Situation) und Netz der zylindrischen Dose - Oberflächeninhalt O (als Funktion des Radius r) - CAS
Hinweis: Beachte, dass in dem Applet Rundungsfehler auftreten können.
Für welchen Radius r wird für eine zylindrische Dose mit einem Volumen von V = 425 cm³ der Oberflächeninhalt minimal?
| Oberfläche = Grundfläche + Mantel + Deckfläche | O = G + M + D = 2·G + M | ▼ |
| Wahl der Bezeichnung für die Variablen r und h: |
|
▼ |
|
Nebenbedingung beachten: Die Höhe h kann aus dem gegebenen Volumen V berechnet werden |
|
▼ |
| Aufstellen der Zielfunktion: |
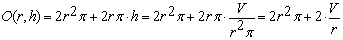
Zielfunktion
Die Bezeichnung O(r) bringt zum Ausdruck, dass die Zielfunktion nur mehr von einer Variablen, nämlich dem Radius r, abhängt . |
▼ |
| Ableiten der Zielfunktion: |
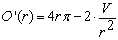 |
▼ |
| 1. Ableitung gleich null setzen: |
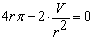 |
▼ |
| Gleichung lösen: |
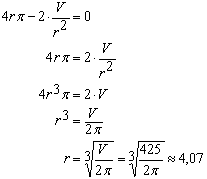
h = 425/4,07² π ≈ 8,14 cm; O(4,07) ≈ 312,93 cm² Allgemein:
Es handelt sich um einen gleichseitigen Zylinder (h = 2r). | ▼ |
| 2. Ableitung für die Unterscheidung von Maximum bzw. Minimum: |
|
▼ |
| Antwort formulieren: |
Der minimale Oberflächeninhalt von 312,93 cm² entsteht für eine zylindrische Dose mit V = 425 cm³ bei einem Radius von r = 4,07 cm. |
Für ein Volumen von V = 1000 cm³ ergibt sich der kleinste Oberflächeninhalt bei einem Radius von r ≈ 5,42 cm.
© 2016 Verlag E. DORNER, Wien; Dimensionen - Mathematik 7; erstellt mit GeoGebra
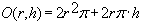
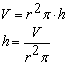
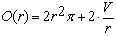
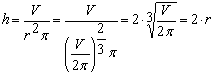
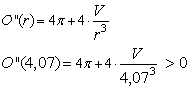 => Minimum
=> Minimum